题意:
对于一个1~n的序列。进行m次区间反转操作;
求最后反转过的区间。
n,m<=100000。
题解:
splay躶题。写完维修数列之后感觉这种题都好写了。
反转啥的打个标记下传就好,记得输出时再Pushdown标记就好了;
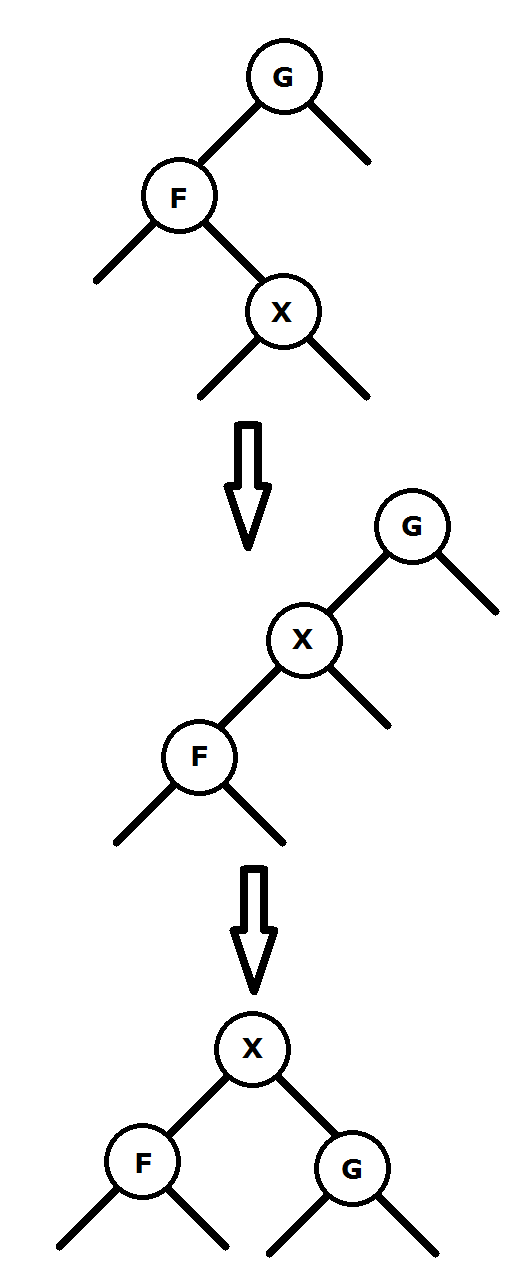
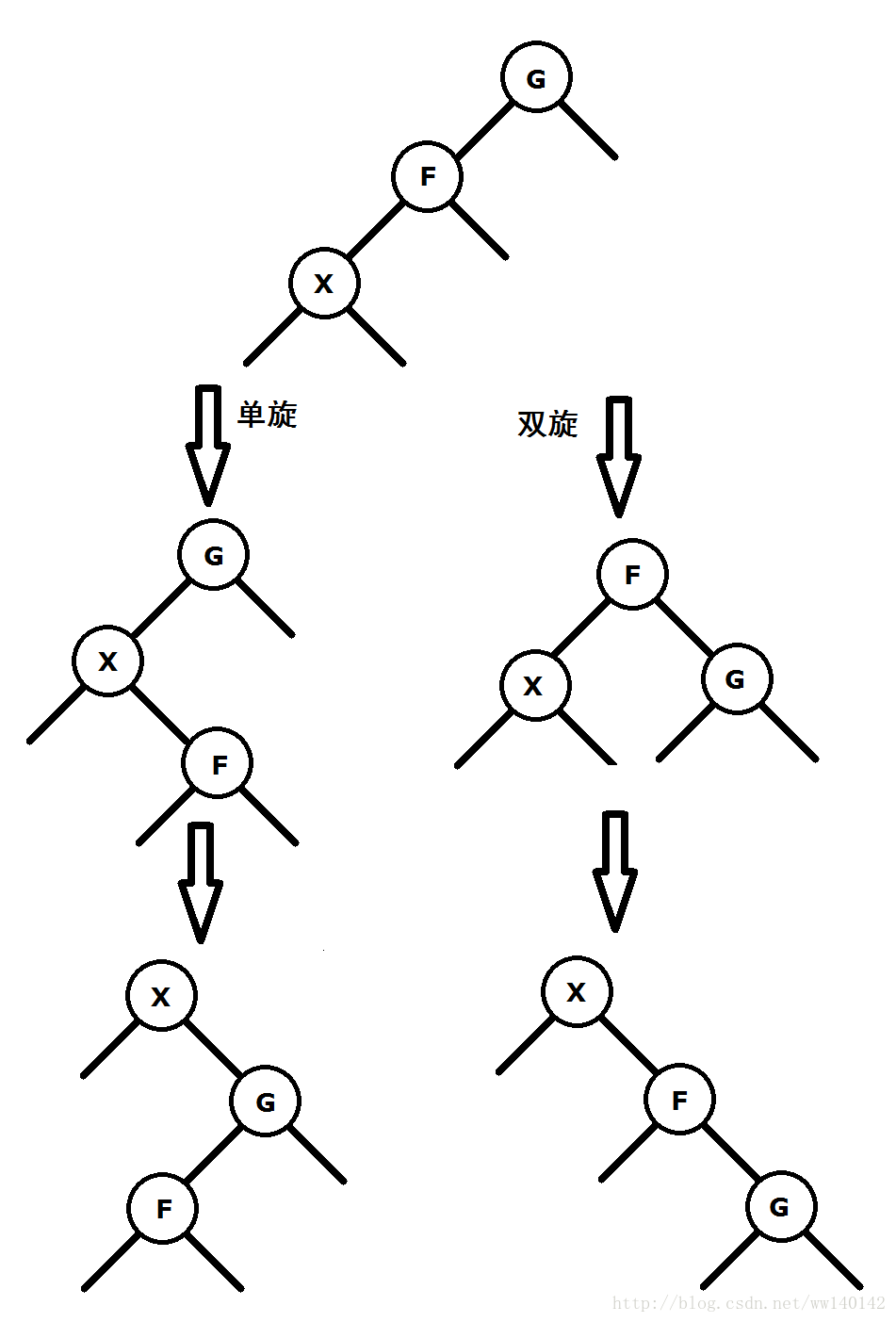
这篇题解就是说一下单旋和双旋的简单差别;
爷爷结点就是目标的情况不讨论了;
zig-zag实际上双旋与单旋的操作是一样的:
不同的是zig-zig操作:
依据某些奇妙的势能分析(),双旋大概比单旋快一些的;
(而且敢写单旋你不怕被各路神犇D吗)
可是经过我的几个小測试,其它函数一样。仅改变单旋双旋,时间并没有太多区别;
下面上为单旋下为双旋;




我就写了这么几道题,可是应该能够发现,不管单双都是能够AC的。
而且仅仅有1588似乎有卡单旋的数据,所以单旋党的猖獗也不是没有道理嘛;
所以单旋双旋对于吾等蒟蒻是随便的的啦= =;
回归正题。
。。发一下3223的代码吧。
代码:
#include#include #include #define N 110001#define which(x) (ch[fa[x]][1]==x)using namespace std;int fa[N],ch[N][2],val[N],size[N],root,tot;bool flag[N];void Pushup(int x){ size[x]=size[ch[x][0]]+size[ch[x][1]]+1;}void Pushdown(int x){ if(flag[x]) { flag[ch[x][0]]^=1; flag[ch[x][1]]^=1; swap(ch[ch[x][0]][0],ch[ch[x][0]][1]); swap(ch[ch[x][1]][0],ch[ch[x][1]][1]); flag[x]=0; }}void Rotate(int x){ int f=fa[x]; bool k=which(x); ch[f][k]=ch[x][!k]; ch[x][!k]=f; ch[fa[f]][which(f)]=x; fa[x]=fa[f]; fa[ch[f][k]]=f; fa[f]=x; Pushup(f); Pushup(x);}/* 单旋spaly void Splay(int x,int g){ while(fa[x]!=g) { Rotate(x); } if(!g) root=x;}*/void Splay(int x,int g)//双旋splay { while(fa[x]!=g) { int f=fa[x]; if(fa[f]==g) { Rotate(x); break; } if(which(x)^which(f)) Rotate(x); else Rotate(f); Rotate(x); } if(!g) root=x;}int Rank(int x,int k){ Pushdown(x); if(k<=size[ch[x][0]]) return Rank(ch[x][0],k); else if(k==size[ch[x][0]]+1) return x; else return Rank(ch[x][1],k-size[ch[x][0]]-1);}int Build(int l,int r,int f){ if(l>r) return 0; int mid=(l+r)>>1,x=++tot; ch[x][0]=Build(l,mid-1,x); ch[x][1]=Build(mid+1,r,x); val[x]=mid; fa[x]=f; Pushup(x); return x;}void Update(int l,int r){ int x,y,t; x=Rank(root,l-1); Splay(x,0); y=Rank(root,r+1); Splay(y,x); t=ch[y][0]; swap(ch[t][0],ch[t][1]); flag[t]^=1;}void Print(int x){ if(!x) return ; Pushdown(x); Print(ch[x][0]); printf("%d ",val[x]); Print(ch[x][1]);}int main(){ int n,m,i,l,r; scanf("%d%d",&n,&m); root=Build(0,n+1,0); for(i=1;i<=m;i++) { scanf("%d%d",&l,&r); Update(l+1,r+1); } Splay(Rank(root,1),0); Splay(Rank(root,n+2),root); Print(ch[ch[root][1]][0]); return 0;}